Free Online Tutorials

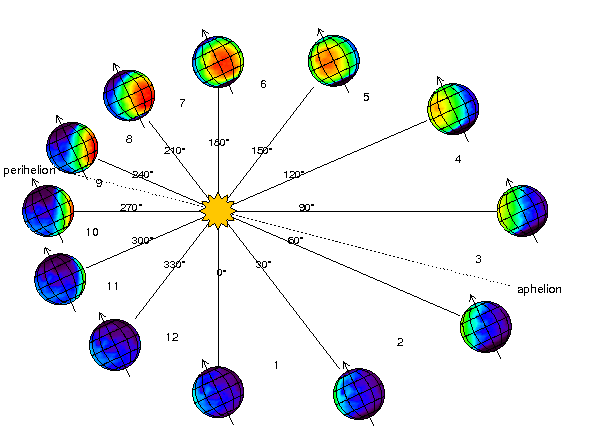
(Copyright image: www-mars.lmd.jussieu.fr)

Method 1:

function SunLongitude1($year, $month, $day, $hour, $min, $sec, $timeZone)
{
    $jdn = gregoriantojd($month, $day, $year) + ($hour + $min / 60 + $sec / 3600) / 24;
    $T = ($jdn - 2451545.5 - $timeZone / 24) / 36525; // Time in Julian centuries from 2000-01-01 12:00:00 GMT
    $T2 = $T * $T;
    $dr = M_PI / 180; // degree to radian
    $M = 357.52910 + 35999.05030 * $T - 0.0001559 * $T2 - 0.00000048 * $T * $T2; // mean anomaly, degree
    $L0 = 280.46645 + 36000.76983 * $T + 0.0003032 * $T2; // mean longitude, degree
    $DL = (1.914600 - 0.004817 * $T - 0.000014 * $T2) * sin($dr * $M);
    $DL = $DL + (0.019993 - 0.000101 * $T) * sin($dr * 2 * $M) + 0.000290 * sin($dr * 3 * $M);
    $L = $L0 + $DL; // true longitude, degree

    // obtain apparent longitude by correcting for nutation and aberration
    $omega = 125.04 - 1934.136 * $T;
    $L = $L - 0.00569 - 0.00478 * sin($omega * $dr);
    $L = $L * $dr;
    return $L = ($L - M_PI * 2 * (floor($L / (M_PI * 2)))) / $dr; // Normalize to (0, 360)
}

Method 2:

function SunLongitude2($year, $month, $day, $hour, $min, $sec, $timeZone)
{
    // Get Julian date for date at noon
    $jd = gregoriantojd($month, $day, $year);
    //correct for half-day offset
    $dayfrac = $hour / 24 - .5;
    //now set the fraction of a day
    $frac = $dayfrac + $min / 60 / 24 + $sec / 3600 / 24 - $timeZone / 24;
    $jd = $jd + $frac;

    // The input to the Atronomer's almanach is the difference between
    // the Julian date and JD 2451545.0 (noon, 1 January 2000)
    $time = ($jd - 2451545);
    // Ecliptic coordinates

    // Mean longitude
    $mnlong = (280.460 + 0.9856474 * $time);
    $mnlong = fmod($mnlong, 360);
    if ($mnlong < 0)
        $mnlong = ($mnlong + 360);

    // Mean anomaly
    $mnanom = (357.528 + 0.9856003 * $time);
    $mnanom = fmod($mnanom, 360);
    if ($mnanom < 0)
        $mnanom = ($mnanom + 360);
    $mnanom = deg2rad($mnanom);

    // Ecliptic longitude and obliquity of ecliptic
    $eclong = ($mnlong + 1.915 * sin($mnanom) + 0.020 * sin(2 * $mnanom));
    $eclong = fmod($eclong, 360);
    if ($eclong < 0)
        $eclong = ($eclong + 360);

    return $eclong;
}

Method 3:

function SunLongitude3($year, $month, $day, $hour, $min, $sec, $timeZone)
{
    $jd = gregoriantojd($month, $day, $year);

    $frac = $hour / 24 + $min / 60 / 24 + $sec / 3600 / 24 - $timeZone / 24;
    $jd = $jd + $frac;

    $d = ($jd - 2451544);

    $w = 282.9404 + 4.70935E-5 * $d; //   (longitude of perihelion)
    $a = 1.000000; //  (mean distance, a.u.)
    $e = 0.016709 - 1.151E-9 * $d; //  (eccentricity)
    $M = 356.0470 + 0.9856002585 * $d; //  (mean anomaly)

    $M = fmod($M, 360);

    // the obliquity of the ecliptic, oblecl:
    $oblecl = 23.4393 - 3.563E-7 * $d;

    //the Sun's mean longitude, L:
    $L = $w + $M;
    $L = fmod($L, 360);

    // the eccentric anomaly
    $E = $M + (180 / M_PI) * $e * sin(deg2rad($M)) * (1 + $e * cos(deg2rad($M)));

    $x = cos(deg2rad($E)) - $e;
    $y = sin(deg2rad($E)) * sqrt(1 - $e * $e);

    $r = sqrt($x * $x + $y * $y);
    $v = rad2deg(atan2($y, $x));

    $lon = $v + $w;
    $lon = fmod($lon, 360);
    if ($lon < 0)
        $lon = ($lon + 360);
    return $lon;
}

Compare the precision of these methods:
We can see in the website: http://www.usno.navy.mil/USNO/astronomical-applications/data-services/earth-seasons, at 03-20-2015 22:45 GMT, longitude of the sun is zero:

echo SunLongitude1(2015, 3, 20, 22, 45, 00, 0); //0.00357264073223 ~ 13''
echo SunLongitude2(2015, 3, 20, 22, 45, 00, 0); //0.00343733553098 ~ 13''
echo SunLongitude3(2015, 3, 20, 22, 45, 00, 0); //0.00785246612753 ~ 28''

Now, we can sort the precision of three methods:

SunLongitude2 > SunLongitude1 > SunLongitude3